Rectangle is one of the 2D object and also quadrilateral regular polygon. It contain four sides. Opposite of the sides are equal in rectangle Image. Rectangle image having four sides. Each side are intersected with 90 degree Two sides are lengths of the rectangle. Two sides are width of the rectangle. In rectangle images Opposite sides of lengths are equal and also opposite sides of width are equal. Rectangular changes should be based on length of the rectangle and width of the rectangle.
Basic Concepts of Rectangle Images:
From the above image AB,BC,CD,DA These are Sides of the rectangle Image.
AB and CD are Parallel sides of the rectangle Images
AB and CD These are Length of the Rectangles
BC and AD These are Width of the rectangle Images
AC and BD Are Diagonals of the Rectangle Images (Rectangle Image Contains Two Diagonal AC and AD .Two Diagonals Are Equal length o f Rectangle Image)
Area and Permeter of Rectangle:
Area of the rectangle:Area of the rectangle is Prodouct of Length and width
Area of rectangle= Length*Width
Perimeter of the rectangle=2(Length + Width)
Example Problems in Rectangle Images:
Ex 1: Find the area of a rectangle whose length is 10m and width is 25 m .
Solution: Area of the rectangle is Product of Length and width
Area of rectangle= Length*Width =10*25, Area = 2500 m^2
Ex 2: Find the Perimeter of the rectangle image?
Solution: Perimeter of the rectangle=2(Length + Width)
From the given image Length =20,width= 5
Perimeter = 2(5+20) =2(25) =50cm
Ex 3: Find the area of a rectangle whose length is 1/2m and width is 8/15 m .
Solution: The area of a rectangle is multiplication of Their length and Width
Length= `1/2` in
Width=`8/15`
Area = Length * width = `1/2 xx 8/15 = 8/30 = 4/15`
Area= `4/15` in^2
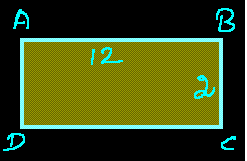
Ex 4: Find the Perimeter of the rectangle image,Their length is 12 and width is 2
Solution: Perimeter of the rectangle=2(Length + Width)
From the given image Length =12,width= 2
Perimeter = 2(12+2) =2(14) =28cm